The problem is solved using conservation of energy. The initial energy is:
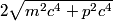 The initial momentum 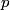 can be found from the definition of relativistic momentum can be found from the definition of relativistic momentum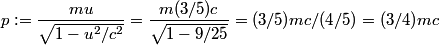 Thus, the initial energy is 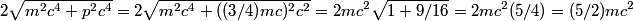 Because there is only mass after the collision, and the total initial momentum is 0, the mass after the collision must be at rest. Therefore its energy is 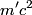 . Equating this with the initial total energy, we find that . Equating this with the initial total energy, we find that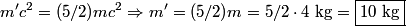 Therefore, answer (D) is the correct answer. |